异常检测
异常检测模型和实例¶
给定一组数据 $x^{(1)}, x^{(2)}, … , x^{(m)}$,我们建立一个模型 $p(x)$,当有一个新的实例 $x_{test}$ 时,如果 $p(x_{test}) \le \epsilon$ 我们就认为 $x_{test}$ 是异常的。
异常检测在网站防盗等领域有广泛的应用,比如我们可以提取用户的一些特征,$x_1$ 代表用户的登录次数,$x_2$ 表示用户游览的页面个数,$x_3$ 表示用户的打字速度,$x_4$ 表示用户的交易次数等等,建立完特征,根据用户的历史数据建立一个模型,当某次用户的行为偏离这个模型较远时,这个用户的帐户可能是被盗了。
另外一个应用领域是在工业制造。比如某个制造飞机引擎的公司,从飞机引擎提取出一系列的特征值,并且训练出一个模型。当新制造出来的引擎符合这个模型时,就可认为是良品,如果偏离这个模型较远时,就可以认为可能有缺陷,需要进一步的检测。
异常检测还在数据中心有广泛的应用,比如可以从一台服务器上提取出一系列特征,如内存占用,CPU 使用率,网络吞吐量,磁盘访问频率等等。利用这些特征建立一个模型。当某个服务器偏离这个模型较远时,可能这台机器快要死机了,就可以进一步查看这台机器的情况以便做出相应的处理。
高斯分布¶
高斯分布也称为正态分布。高斯分布有两个参数,一个是平均值 $\mu$,另外一个是方差 $\sigma^2$ ($\sigma$ 称为标准差),给定一个数值 X 作为横轴,它出现在不同位置的概率作为 Y 轴,在二维坐标上画出的图形是一个“钟形”的图形。
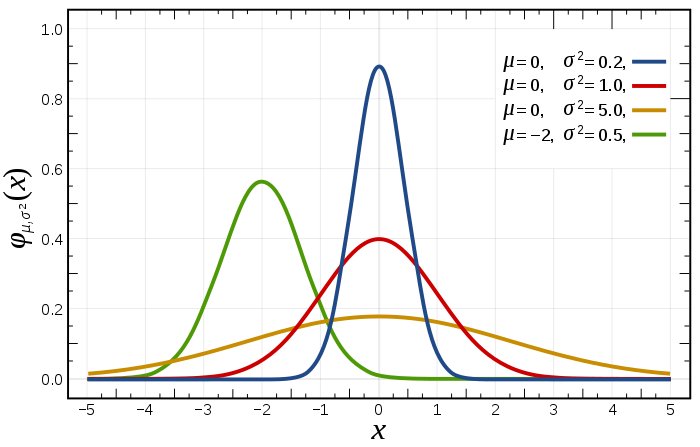
用数据公式给出高斯分布的公式如下:
$$ p(x; \mu, \sigma^2) = \frac{1}{\sigma \sqrt{2\pi}} exp \left( - \frac{(x - \mu)^2}{2 \sigma^2} \right) $$
参数计算¶
假设我们有一个数据集 $x^{(1)}, x^{(2)}, … , x^{(m)}$,其中 $x^{(i)} \in R$。且 $x^{(i)}$ 满足高斯分布,记作 $x^{(i)} \sim N(\mu, \sigma^2)$,如何算出高斯分布的参数 $\mu, \sigma^2$ 呢?
算法可以用下面的公式给出:
$$ \mu = \frac{1}{m} \sum_{i=1}^m x^{(i)} $$
$$ \sigma^2 = \frac{1}{m} \sum_{i=1}^m (x^{(i)} - \mu)^2 $$
这个实际上就是概率论里的极大似然法来估计参数。另外需要提一点,计算方差 $\sigma^2$ 的公式里,一些概率论书本里分母是用 $m-1$,但机器学习领域喜欢直接用 $m$ ,虽然这是两个不同版本的公式,但在实际应用中,如果样例个数足够多,即 m 很大的话,实际计算结果差别不大。
异常检测算法¶
假设我们有一个数据集 $x^{(1)}, x^{(2)}, … , x^{(m)}$,其中 $x^{(i)} \in R^n$,其中每个特征都独立地满足高斯分布,即 $x_j^{(i)} \sim N(\mu_j, \sigma_j^2)$。那么高斯分布的概率密度函数为:
$$ p(x) = \prod_{j=1}^n p(x_j; \mu_j, \sigma_j^2) $$
其中 $\prod$ 是连乘符号,表示其后的式子相乘。
利用高斯分布进行异常检测的算法可以完整地描述如下:
- 特征选择。选择那些能鉴别出异常的特征 $x_j$。
- 针对每个特征,计算出其高斯分布参数 $\mu_j, \sigma_j^2$。计算公式为:
$$ \mu_j = \frac{1}{m} \sum_{i=1}^m x_j^{(i)} $$
$$ \sigma_j^2 = \frac{1}{m} \sum_{i=1}^m (x_j^{(i)} - \mu_j)^2 $$
- 给定一个新的实例 $x$,计算其出现的概率 $p(x)$。计算公式为:
$$ p(x) = \prod_{j=1}^n p(x_j; \mu_j, \sigma_j^2) = \prod_{j=1}^n \frac{1}{\sigma_j \sqrt{2\pi}} exp \left( - \frac{(x_j - \mu_j)^2}{2 \sigma_j^2} \right) $$
- 选定一个较小的常数 $\epsilon$,如果 $p(x) \le \epsilon$ 则表示新的实例 $x$ 是异常的。
异常检测算法的性能评价¶
怎么样评价一个异常检测算法的性能是否达到要求呢?
假设我们拿飞机引擎制造作为例子,我们有 10,000 个正常的引擎数据,20 个异常的引擎数据。这样我们把数据分成三份:
- 训练数据集:6,000 个正常的引擎数据
- 交叉验证数据集:2,000 个正常的引擎数据;10 个异常引擎数据
- 测试数据集:2,000 个正常的引擎数据;10 个异常的引擎数据
接下来我们开始来评估算法的性能
- 使用训练数据集来建立 $p(x)$ 模型
- 使用下面的模型来预测交叉验证数据集和测试数据集里的样例
$$ y = \begin{cases} 1, & if p(x) < \epsilon (异常)\\ 0, & if p(x) \ge \epsilon (正常) \\ \end{cases} $$
- 使用交叉验证数据集来计算查准率,召回率以及$F_1Score$
$$ Precision = \frac{TruePositive}{TruePositive + FalsePositive} $$
$$ Recall = \frac{TruePositive}{TruePositive + FalseNegative} $$
$$ F_1Score = 2 \frac{PR}{P + R} $$
- 使用交叉验证数据集来选择合适的 $\epsilon$,来让 $F_1Score$ 的值最大
- 最后使用测试数据集来计算模型的最终性能 $F_1Score$
TruePosition: 真阳性,即真实结果是真,算法的预测结果也是真 FalsePositive: 假阳性,即真实结果是假,算法的预测结果是真 FalseNegative: 假阴性,即真实结果是真,算法的预测结果是假
异常检测与监督学习的区别¶
上一节介绍的飞机引擎异常检测算法里,我们有正常的数据,有异常的数据,为什么不直接用逻辑回归或神经网络算法来对一个新引擎进行直接预测呢?实际上异常检测和监督学习有其不同的适用范围。
异常检测适用范围
- 正向样本 (y = 1) 非常少 (0 - 20),但负向样本 (y = 0) 很多
- 有太多的异常类型,算法很难从正常的数据样例里学习到异常的特征
- 未来新出来的异常数据和我们训练样例里现有的异常数据根本不一样,即没见过的异常样例
如果满足这三个条件中的任何一个,都需要考虑使用异常检测算法,而不是监督学习相关的算法。监督学习算法适用于有大量的正向样本,也有大量的负向样本,有足够的正向样本让算法来学习其特征,未来新出现的正向数据可能和训练样例里的某个正向样本类似。
由此可见异常检测和监督学习相关算法的适用范围是不一样的。下面是一些例子
| 异常检测 | 监督学习 |
|---|---|
| 信用卡诈骗 | 垃圾邮件识别 |
| 制造业异常产品检测 | 天气预报 (晴/雨 等) |
| 数据中心机器异常检测 | 癌症检测 |
异常检测中的特征选择¶
非高斯分布特征的转换
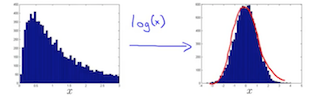
使用高斯分布来作为异常检测模型时,有个前提,即每个特征都需要独立地呈现高斯分布。如果我们获得的特征数据可视化后发现他不是一个高斯分布的钟形图形怎么办呢?我们可以用 octave 的 hist 命令来画出特征的柱状图,然后对特征进行转换,比如画出 $log(x)$ 的图形,或画出 $x^{0.5}$ 或 $x^{0.1}$ 的柱状图。看图形的形状来判断是否符合高斯分布。然后选择转换后的特征来加入我们的异常检测算法中来。
异常检测的错误分析
假如我们有一个异常检测算法,算出正常样本的概率很大,但算出异常样本的概率也很大。这样就没有办法区分出异常样本了。这个时候,一个可行的方法是去查看这个概率很大的异常样本,看能不能得到一些启发,以便让我们发现一些新的特征,用这个特征可以把这种异常样本区分出来。
特征选择的一般性原则
选择那些在异常时,特征值会变得很大或很小的特征来作为异常检测的特征。比如,我们要检测数据中心中的计算机工作是否正常,我们有下面几个特征:
- CPU 使用率
- 网络吞吐量
- 磁盘访问速度
- 内存使用情况
一般情况下,CPU 使用率和网络吞量是成正比的,即用户访问越多,CPU 使用率就越高。当 CPU 使用率很高,但网络吞吐量比较小时,这个时候这个机器可能就出现异常了,比如进入了死循环了。如果我们想检测出这种异常,可以选择 CPU 使用率 / 网络吞吐量 来作为一个新的特征,加入我们的异常检测算法里。