零基础学习朴素贝叶斯算法
朴素贝叶斯¶
朴素贝叶斯 (Naive Bayers) 是一种基于概率统计的分类方法,它在条件独立假设的基础上,使用贝叶斯定理构建算法,在文本处理领域有广泛的应用。
1 算法原理¶
要讲清楚算法原理,我们需要先搞清楚贝叶斯定理,它是一个条件概率公式。
1.1 贝叶斯定理¶
我们来看一下维基百科上一个有意思的例子。警察使用一个假冒伪劣的呼气测试仪来测试司机是否醉驾。假设这个仪器有 5% 的概率会把一个正常的司机判断为醉驾,但对真正醉驾的司机,则其测试结果是 100% 准确的。从过往的统计得知,大概有 0.1% 的司机为醉驾。假设,警察随机拦下一个司机,让他 (她) 做呼气测试,仪器测试结果为醉驾。仅凭这一结果判断,这位倒霉的司机真的醉驾的概率是多高?
90% ?50% ?真实的结果是不到 2% 。对,你没看错,如果我们没有通过其他的方法(比如闻司机身上的酒味),单单凭这个仪器的测试结果来判断,其实准确性是非常低的。
假设,我们的样本里有 1000 人,根据过往的统计数据,这 1000 位司机里有 0.1% 的概率为真正醉驾,即有 1 位真正醉驾的司机,999 位正常。这 1000 位司机均拿这个劣质呼气测试仪来测试,则有多少人会被判断为醉驾?对这位真正醉驾的司机,他 (她) 无法蒙混过关,而对 999 位正常的司机,有 5% 的概率会被误测,所以总共有 1 + 999 x 5% 个倒霉蛋会被仪器判断为醉驾。由此可得,所有被仪器判断为醉驾的司机里面,真正醉驾的概率是 1 / (1 + 999 x 5%) = 1.96% 。
实际上,贝叶斯定理是计算这类条件概率问题的绝佳方法。我们记 P(A|B) 表示观察到事件 B 发生时,事件 A 发生的概率,则贝叶斯定理的数学表达为:
$$ P(A|B) = \frac {P(A) P(B|A)} {P(B)} $$
回到我们的例子里,我们记事件 A 为司机真正醉驾,事件 B 为仪器显示司机醉驾。则我们的例子里要求解的问题即为 P(A|B),即观察到仪器显示司机醉驾(事件 B 发生)时,司机真正醉驾(事件 A 发生)的概率是多少。P(A) 表示司机真正醉驾的概率,这是先验概率,例子里的数值是 0.1% 。P(B|A) 表示当司机真正醉驾时(事件 A 发生),仪器显示司机醉驾(事件 B 发生)的概率是多少,从例子里的数据得知是 100% 。P(B) 表示仪器显示司机醉驾的概率,这里有两部分的数据,针对真正醉驾的司机 (0.1%),仪器能 100% 检测出来,故这部分的数值上 0.1% x 100%;针对正常的司机 (1 - 0.1%) ,仪器显示醉驾的概率为 (1 - 0.1%) * 5%。代入贝叶斯定理即可得:
P(A|B) = 0.1% x 100% / [0.1% x 100% + (1 - 0.1%) * 5%] = 1.96%
1.2 朴素贝叶斯分类法¶
假设我们有一个己标记的数据集 $[x^{(i)}, y^{(i)}]$ ,其中 $y^{(i)} \in [C_1, C_2,…, C_b]$,即数据集总共有 b 个类别;$x^{(i)} = [x_1, x_2,…, x_n]$,即总共有 n 个输入特征。针对一个新的样本 $x$ ,我们要预测 $y$ 的值,即对 $x$ 进行分类。这是个典型的机器学习里的分类问题。
我们要求解的问题,使用统计学的语言,可以描述为,当观察到输入样本是 $x$ 时,其所属于的类别 $y = C_k$ 的概率,使用条件概率公式可以写成:
$$ p(C_k|x) $$
其中 $C_k \in [C_1, C_2,…, C_b]$ ,我们只需要分别求出所有 b 个类别的概率,然后取概率最大的那个 $C_k$ 即是 $x$ 所属的类别。直接求解上述公式比较困难,我们应用贝叶斯定理进行一次变换:
$$ p(C_k|x) = \frac {p(C_k) P(x|C_k)} {P(x)} $$
针对不同的 $C_k$ ,$P(x)$ 都是固定的值。故,我们只需要求解,针对不同的 $C_k \in [C_1, C_2,…, C_b]$ 的情况下,$p(C_k) P(x|C_k)$ 的最大值即可知道,$x$ 属于哪个类别。即:
$$ p(C_k|x) \varpropto p(C_k) P(x|C_k) $$
其中 $\varpropto$ 表示成正比的意思。根据联合概率公式,可得:
$$ p(C_k) P(x|C_k) = P(C_k, x) $$
对概率统计陌生的同学不要被专有术语吓到了,联合概率表示的是一种概率叠加。比如,你走在路上遇到美女是一个随机事件,美女对你一见钟情是另外一个随机事件,那么你在路上遇到美女,且对你一见钟情的概率要怎么计算呢?即 P(美女,对你一见钟情) 的值是多少呢?使用概率叠加来计算,遇到美女的概率,乘以是个美女,且对你一见钟情的概率(条件概率)。即:
$$ P(美女,对你一见钟情) = P(美女) P(对你一见钟情|美女) $$
我们从白日梦回到枯燥的数学。又因为,$x$ 是有 n 个特征向量,即 $x = [x_1, x_2,…, x_n]$ ,可得:
$$ p(C_k) P(x|C_k) = P(C_k, x) = P(C_k, x_1, x_2,…, x_n) $$
根据链式法则以及条件概率的定义,我们可以进一步推导公式:
$$ P(C_k, x_1, x_2,…, x_n) = P(x_1, x_2,…, x_n, C_k) $$
$$ P(x_1, x_2,…, x_n, C_k) = P(x_1 | x_2,…, x_n, C_k) P(x_2,…, x_n, C_k) $$
$$ P(x_1, x_2,…, x_n, C_k) = P(x_1 | x_2,…, x_n, C_k) P(x_2 | x_3,…, x_n, C_k) … P(x_n | C_k) P(C_k) $$
咦,好像越推导越复杂了。是时候用上我们的法宝了。上述推导里,我们只用了贝叶斯定理,我们的法宝就是前面的定语朴素。朴素指的是条件独立假设,即事件之间没有关联关系。比如,掷一个质地均匀的骰子两次,前后之间出现的数字是独立的,不相关的,我们称这两个事件是条件独立的。朴素贝叶斯算法的前提是,输入特征需要满足条件独立假设。即,当 $i \neq j$ 时,$x_i$ 和 $x_j$ 是不相关的,用大白话说,就是 $x_i$ 事件是否发生和 $x_j$ 没关系。根据条件独立的原则:
$$ P(x_i | x_{i+1},…, x_n, C_k) = P(x_i | C_k) $$
有了这个公式,我们就可以简化为:
$$ P(x_1, x_2,…, x_n, C_k) = P(x_1 | C_k) P(x_2 | C_k) … P(x_n | C_k) P(C_k) $$
这样我们的最终推导结果就是:
$$ p(C_k|x) \varpropto P(C_k) \prod_{i=1}^n P(x_i | C_k) $$
其中 $\prod$ 是连乘符号。$P(C_k)$ 表示每种类别出现的概率,这个值很容易从数据集里统计出来。$P(x_i | C_k)$ 表示当类别为 $C_k$ 时,特征 $x_i$ 出现的概率,这个也可以从数据集中统计出来。这就是朴素贝叶斯分类法的数学原理。
2 一个简单的例子¶
我们先通过一个简单的例子,来看怎么样应用朴素贝叶斯分类法。假设我们有以下的关于驾龄,平均车速和性别的统计数据:
| 序号 | 驾龄 | 平均车速 | 性别 |
|---|---|---|---|
| 1 | 1 | 60 | 男 |
| 2 | 2 | 80 | 男 |
| 3 | 3 | 80 | 男 |
| 4 | 2 | 80 | 男 |
| 5 | 1 | 40 | 男 |
| 6 | 2 | 40 | 女 |
| 7 | 1 | 40 | 女 |
| 8 | 1 | 40 | 女 |
| 9 | 3 | 60 | 女 |
| 10 | 3 | 80 | 女 |
现在观察到一个驾龄为 2 年的人,平均车速为 80,问:这个人的性别是什么?
假设 $C_0$ 表示女,$C_1$ 表示男,$x_0$ 表示驾龄,$x_1$ 表示平均车速。我们先来计算这个人为女性的概率相对值。根据统计数据,女性司机的概率 $P(C_0) = 5 / 10 = 0.5$。根据统计数据,驾龄为 2 年的女性司机的概率,即 $P(x_0 | C_0) = 1 / 10 = 0.1$。平均车速为 80 的女性司机的概率 $P(x_1 | C_0) = 1 / 10 = 0.1$。根据朴素贝叶斯分类法的数学公式:
$$ P(C_0) \prod_{i=1}^n P(x_i | C_0) = 0.5 \times 0.1 \times 0.1 = 0.005 $$
接着,我们来计算这个人为男性的概率相对值。根据统计数据,不难得出男性司机的概率 $P(C_1) = 5 / 10 = 0.5$。驾龄为 2 年的男性司机的概率 $P(x_0 | C_1) = 2 / 10 = 0.2$。平均车速为 80 的男性司机的概率 $P(x_1 | C_1) = 3 / 10 = 0.3$。根据朴素贝叶斯分类法的数学公式:
$$ P(C_1) \prod_{i=1}^n P(x_i | C_0) = 0.5 \times 0.2 \times 0.3 = 0.03 $$
从相对概率来看,这个人是男性的概率,是这个人是女性的概率的 6 倍,据此我们判断这个人是男性。我们也可以从相对概率里算出绝对概率,即这个人是男性的概率是 $0.03 / (0.03 + 0.005) = 0.857$ 。
3 概率分布¶
到目前为止,我们介绍的朴素贝叶斯分类法,是根据数据集里数据,计算出绝对概率来进行求解。再看一遍朴素贝叶斯分类法的数学公式:
$$ p(C_k|x) \varpropto P(C_k) \prod_{i=1}^n P(x_i | C_k) $$
其中,$P(x_i | C_k)$ 表示在类别 $C_k$ 里,特征 $x_i$ 出现的概率。这里面有个最大的问题,如果数据集太小,那么从数据集里计算出来的概率偏差将非常严重。举个例子,你观察到一个质地均匀的骰子投掷 6 次的结果是 [1, 3, 1, 5, 3, 3]。质地均匀的骰子,每个点出现的概率都是 1/6 ,如果你根据我们观察到的数据集,去计算每个点的概率,和真实的概率相差将是非常大的。
怎么解决这个问题呢?答案是使用概率分布来计算概率,而不从数据集里计算概率。为了介绍清楚这个问题,需要从概率统计的基本概念谈起,那些对概率统计比较熟悉的读者可以直接跳过本节内容。
3.1 概率统计的基本概念¶
人的身高是一个连续随机变量,而投掷一个骰子得到的点数则是一个离散随机变量。我们闭着眼睛在地球上随便抓一个人,问:这个人身高是 170 cm 的可能性是多大呢?如果有一个函数 $f(x)$,能描述人类身高的可能性,那么直接把 170 cm 代入即可求出这个可能性。这个函数就是概率密度函数,也称为 PDF (Probability Density Function)。典型的概率密度函数是高斯分布函数,比如人类的身高,就满足高斯分布的规律,我们在下文会详细介绍。
再比如,投掷一个质地均匀的骰子,得到 6 的概率是多少?大家应该都知道答案是 1/6 。假如有一个函数 $f(x)$,能描述骰子出现 x 点数($x \in [1, 6]$)的概率,那么把 x 代入即可得到概率,这个函数称为概率质量函数,即 PMF (Probability Mass Function)。为什么要费力使用概率质量函数呢?一是在数学追求统一性,二是并不是所有的离散随机变量的概率分布,都像投掷一次骰子这么直观。比如投掷 6 次质地均匀的骰子,得到 4 个 4 的概率是多少?相信好学的你会限入无限的沉思,并感叹一下:这个问题不好算啊。这个时候如果有概率质量函数,就可轻松求解啦。
总结一下,随机变量分成两种,一种是连续随机变量,另外一种是离散随机变量。概率密度函数描述的是连续随机变量在某个特定值的可能性,概率质量函数描述的是离散随机变量在某个特定值的可能性。而概率分布则是描述随机变量取值的概率规律。
3.2 多项式分布¶
抛一枚硬币,要么出现正面,要么出现反面(我们假设硬币不会立起来)。假如出现正面的概率是 p ,则出现反面的概率就是 1 - p 。符合这种规律的概率分布,称为伯努利分布 (Bernoulli Distribution)。其概率质量函数为:
$$ f(k ; p) = p^k (1-p)^{1-k} $$
其中,$k \in [0, 1]$,p 是出现 1 的概率。比如,抛一次质地均匀的硬币,得到正面的概率为 0.5,这是众所周知的答案。我们代入上述公式,也可以得到相同的结果,即 $f(1 ; 0.5) = 0.5$。
更一般的情况,即不止两种可能性时,假设每种可能性是 $p_i$,则满足 $\sum_i^n p_i = 1$ 条件的概率分布,我们称为类别分布 (Categorical Distribution)。比如我们投掷一个骰子,则会出现 6 种可能性,所有的可能性加起来概率为 1。类别分布的概率质量函数为:
$$ f(x | p) = \prod_{i=1}^k p_i^{x_i} $$
$\prod$ 是我们见过的连乘符号。其中,$k$ 是类别的数量,$p_i$ 是第 i 种类别的概率,$x_i$ 当且仅当类别 x 为类别 i 时,其值为 1,其他情况其值为 0。比如,针对质地均匀的骰子,$k$ 的值为 6,$p_i$ 的值为 1/6 。问,投掷这个骰子得到 3 的概率是多少?傻子都知道,答案是 1/6 啊。我们代入概率质量函数验算一下,$f(3 | p) = \prod_{i=1}^6 p_i^{x_i}$,针对所有 $i \neq 3$ 的情况,$x_i = 0$,针对 $i = 3$ 的情况,$x_i = 1$,所以容易算出 $f(3 | p) = 1/6$。
停停停,你都快把我绕晕了,这么简单的问题为什么要弄得这么复杂呢?笔者仿佛听到读者在报怨了。前面都是铺垫,接下来介绍的内容才是精华。再往下看,你就就能知道我们把问题复杂化的原因,也能看到数学之美。
那我们开始吧,问:抛一枚质地均匀的硬币 10 次,出现 3 次正面的概率是多少?这是个典型的二项式分布问题。二项式分布,指的是把符合伯努利分布的实验做了 n 次,结果 1 出现 0 次,1 次,2 次 … n 次的概率分别是多少,它的概率质量函数为:
$$ f(k; n, p) = \frac {n!}{k! (n-k)!} p^k (1 - p)^{n-k} $$
其中,k 是结果 1 出现的次数,$k \in [0, 1, …, n]$,n 是实验的总次数,p 是在一次实验中结果 1 出现的概率。怎么理解这个公式呢?我们总共进行了 n 次实验,那么出现 k 次结果 1 的概率为 $p^k$ ,剩下的必定是结果 0 的次数,即出现了 n - k 次,其概率为 $(1 - p)^{n-k}$,公式前面的系数表示的是组合,即 k 次结果 1 可以是任意的组合,比如可能是前 k 次是结果 1,也可能是最后 k 次出现的是结果 1。回到最初的问题:抛一枚质地均匀的硬币 10 次,出现 3 次正面的概率是多少?代入二项式分布的概率质量函数,得到:
$$ f(3; 10, 0.5) = \frac {10!} {3! \times (10 - 3)!} \times 0.5^3 \times (1 - 0.5)^{10 - 3} = 0.1171875 $$
我们再看一个更简单的例子,问:抛一枚质地均匀的硬币 1 次,出现 0 次正面的概率是多少?代入二项式分布的概率质量函数,得到:
$$ f(0; 1, 0.5) = \frac {1!} {0! \times (1 - 0)!} \times 0.5^0 \times (1 - 0.5)^{1 - 0} = 0.5 $$
其中,零的阶乘为 1,即 $0! = 1$。结果跟我们预期的相符,当实验只做一次时,二项式分布退化为伯努利分布。
多项式分布是指满足类别分布的实验,连续做 n 次后,每种类别出现的特定次数组合的概率分布情况。假设,$x_i$ 表示类别 i 出现的次数,$p_i$ 表示类别 i 在单次实验中出现的概率。当满足前提条件 $\sum_{i=1}^k x_i = n$ 时,由随机变量 $x_i$ 构成的随机向量 $X = [x_1,…,x_k]$ 满足以下分布函数:
$$ f(X,n,P) = \frac {n!}{\prod_{i=1}^k x_i!} \prod_{i=1}^k p_i^{x_i} $$
其中,P 是由各个类别的概率构成的向量,即 $P = [p_1,…,p_k]$,k 表示类别的总数,n 表示实验进行的总次数。理解这个公式也比较简单,可以把 $\prod_{i=1}^k p_i^{x_k}$ 理解为,按照特定顺序,所有类别出现的某个特定的次数组合的概率,比如投掷骰子 6 次,出现 (1, 2, 3, 4, 5, 6) 这样特定顺序组合的概率。前面的系数,表示组合的个数,比如,投掷骰子 6 次,每个点数都出现一次,可以是 (1, 2, 3, 4, 5, 6) ,也可以是 (1, 3, 2, 4, 5, 6) 。
我们看一个例子,同时投掷 6 个质地均匀的骰子,出现 (1, 2, 3, 4, 5, 6) 这种组合的概率是多少?我们可以把这个问题转换成,连续投掷 6 次质地均匀的骰子,每个类别都出现 1 次的概率。这是个典型的多项式分布问题,其中随机向量 $X = [1, 1, 1, 1, 1, 1]$,代入多项式分布的概率质量函数可得:
$$ f(X,n,P) = \frac {6!}{\prod_{i=1}^6 1!} \prod_{i=1}^6 (1/6) = 0.015432099 $$
好了,是时候解决之前那个让你挠耳抓腮的问题了:投掷 6 次质地均匀的骰子,得到 4 个 4 的概率是多少?我们需要把这个问题转换为二项式分布问题。投掷 1 次骰子时,得到 4 的概率是 1/6,得到其他点数 (非 4) 的概率是 5/6。现在需要计算投掷 6 次骰子,得到 4 个 4 的概率,代入二项式分布的概率质量函数可得:
$$ f(4; 6, 1/6) = \frac {6!}{4! \times (6 - 4)!} (1/6)^4 \times (1 - 1/6)^{6 - 4} = 0.008037551 $$
我们再来算一下,同时投掷 6 个质地均匀的骰子,出现 5 个 1 的概率是多少?还是转换为二项式分布问题:
$$ f(5; 6, 1/6) = \frac {6!}{5! \times (6 - 5)!} (1/6)^5 \times (1 - 1/6)^{6 - 5} = 0.000643004 $$
在厦门和台湾,中秋博饼是一个盛大的传统活动,相传是郑成功为了缓解士兵的中秋思乡之情,发明的一种游戏。很多公司在中秋节都会组织员工博饼,奖品从牙膏,牙刷,洗衣粉,食用油到洗发水,购物卡,生活用品样样俱有。往往这个时候员工都会玩得很开心。其规则是,所有参与的玩家轮流,同时投掷 6 个骰子,根据掷出的不同点数组合,发放对应奖项的奖品。游戏设有一个状元,两个对堂,以及其他数量不等的不同名目的奖项。状元的点数组合是 4 个 4 或者 6 个 4 或者 5 个相同点数的骰子组合,如 5 个 1,5 个 2 等。如果是顺子,即 (1, 2, 3, 4, 5, 6) 的组合,则为对堂。玩过中秋博饼的读者经常会有这样的体会,状元奖品早就被博走了,可是对堂奖品却还有,今天我们从概率的角度来看看为什么会出现这个现象。根据上文例子的计算结果,出现对堂的概率是 0.015432099,而出现状元的概率是 0.008037551 + 6 x 0.000643004 = 0.011895575(我们忽略 6 个 4 的超级状元组合)。说明古人在发明这种游戏时,还是充分考虑过概率的,即博出状元的概率还是比对堂要低。不过,由于对堂有两份奖品,算起来,虽然对堂出现的概率比状元高,但需要出现两次才能把全部对堂的奖品消耗完,而其概率又不足状元的两倍。这就解释了,为什么往往状元已经被博走了,可是还有对堂奖品的原因。
简单总结一下,二项式分布,描述的是,多次伯努利实验中,某个结果出现次数的概率。多项式分布,描述的是,多次进行满足类别分布的实验,所有类别出现的次数组合的分布。
二项式分布和多项式分布,结合朴素贝叶斯算法,经常被用来实现文章分类算法。比如,有一个论坛需要对用户的评论进行过滤,屏蔽掉不文明的评论。首先,我们需要有一个经过标记的数据集,我们称为语料库。假设,我们使用人工标记的方法,对评论进行人工标记,标记为 1 表示包含不文明用语的评论,标记为 0 表示正常评论。
假设我们的词库大小为 k ,则文章里出现的某个词,可以看成是一次满足 k 个类别的类别分布实验。我们知道,一篇评论是由 n 个词组成的,故一篇文章可以看成是进行 n 次符合类别分布的实验后的产物。由此得知,一篇评论文章服从多项式分布,它是词库里的所有词语出现的次数组合构成的随机向量。一般情况下,词库比较大,评论文章只是由少量词组成,所以这个随机向量是很稀疏的,即大部分元素为零。通过分析语料库,我们容易统计出每个词出现不文明评论以及正常评论文章里的概率,即 $p_i$ 的值。同时,针对待预测的评论文章,我们可以统计出词库里的所有词在这篇文章里的出现次数,即 $x_i$ 的值;以及评论文章的词语个数 n 。代入多项式分布的概率质量函数:
$$ f(X,n,P) = \frac {n!}{\prod_{i=1}^k x_i!} \prod_{i=1}^k p_i^{x_i} $$
我们可以求出,待预测的评论文章构成的随机向量 X ,其为不文明评论的相对概率。同理也可求出其为正常评论的相对概率,通过比较两个相对概率,就可以对这篇文章输出一个预测值。当然,实际应用中,涉及到大量的自然语言处理的手段,包括中文分词技术,词的数学表示等。在此不一一展开。
3.3 高斯分布¶
在车速和性别预测的例子里,我们的平均车速,笔者故意给出了离散值,实际上它是一个连续值。这个时候怎么用朴素贝叶斯算法来处理呢?答案是,可以用区间来把连续值转换为离散值。比如,我们把 [0, 40] 之间的平均车速作为一个级别,把 [40, 80] 之间的平均车速作为另外一个级别,此外再把 80 以上的车速作为另外一个级别。这样就可以把连续的值变成离散的值,从而使用朴素贝叶斯分类法进行处理。另外一个方法,是使用连续随机变量的概率密度函数,把数值转换为一个相对概率。本节介绍的高斯分布就是这样的方法。
高斯分布 (Gaussian Distribution) 也称为正态分布 (Normal Distribution),是自然界最常见的一种概率密度函数。人的身高满足高斯分布,特别高和特别矮的人出现的相对概率都比较低。人的智商也符合高斯分布,特别聪明的天才和特别笨的人出现的相对概率都比较低。高斯分布的概率密度函数为:
$$ f(x) = \frac {1} {\sqrt {2 \pi \sigma^2}} \exp \left( - \frac {(x - \mu)^2} {2 \sigma^2} \right) $$
其中 x 为随机变量的值,$f(x)$ 为随机变量的相对概率,$\mu$ 为样本的平均值,其决定了高斯分布曲线的位置,$\sigma$ 为标准差,其决定了高斯分布的幅度,其值越大,分布越分散,值越小,分布越集中。典型的高斯分布如图 9-1 所示:
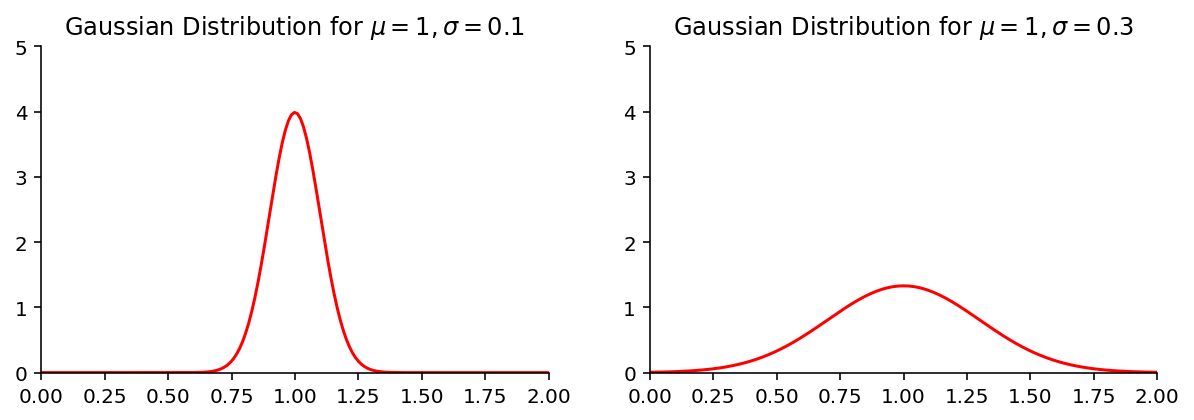
这里需要提醒读者注意,高斯分布的概率密度函数和支持向量机里的高斯核函数的区别。二者的核心数学模型是相同的,但目的不同。
4 连续值的处理¶
我们来看一个来自维基百科的例子。假设,我们有一组人类身体特征的统计数据如下:
| 性别 | 身高(英尺) | 体重(磅) | 脚掌(英寸) |
|---|---|---|---|
| 男 | 6 | 180 | 12 |
| 男 | 5.92 | 190 | 11 |
| 男 | 5.58 | 170 | 12 |
| 男 | 5.92 | 165 | 10 |
| 女 | 5 | 100 | 6 |
| 女 | 5.5 | 150 | 8 |
| 女 | 5.42 | 130 | 7 |
| 女 | 5.75 | 150 | 9 |
假设某人身高 6 英尺、体重 130 磅、脚掌 8 英寸,请问此人的性别是什么?
根据朴素贝叶斯公式:
$$ p(C_k|x) \varpropto P(C_k) \prod_{i=1}^n P(x_i | C_k) $$
针对待预测的这个人的数据 x,我们只需要分别求出男性和女性的相对概率:
$$ p(性别) \times p(身高|性别) \times p(体重|性别) \times p(脚掌|性别) $$
然后取相对概率较高的性别为预测值即可。这里的困难在于,所有的特征都是离散变量,无法根据统计数据计算概率。当然,这里我们可以用区间法,把连续变量转换为离散变量,然后再计算概率。由于数据量较小,这显然不是个好方法。由于人类身高,体重,脚掌尺寸满足高斯分布,故一个更好的办法,是使用高斯分布的概率密度函数来求相对概率。
首先,针对男性和女性,分别求出每个特征的平均值和方差:
| 性别 | 身高均值 | 身高方差 | 体重均值 | 体重方差 | 脚掌均值 | 脚掌方差 |
|---|---|---|---|---|---|---|
| 男性 | 5.855 | 3.5033e-02 | 176.25 | 1.2292e+02 | 11.25 | 9.1667e-01 |
| 女性 | 5.4175 | 9.7225e-02 | 132.5 | 5.5833e+02 | 7.5 | 1.6667e+00 |
接着,我们利用高斯分布的概率密度函数,来求解男性身高为 6 英尺的相对概率:
$$ p(身高=6|男性) = \frac {1} {\sqrt {2 \pi \times 3.5033e-02}} \exp \left( - \frac {(6 - 5.855)^2} {2 \times 3.5033e-02^2} \right) \approx 1.5789 $$
这里的关键是,把连续值(身高)作为输入,通过高斯分布的概率密度函数的处理,直接转换为相对概率。注意,这里是相对概率,所以其值大于 1 并未违反概率论规则。
我们使用相同的方法,容易算出以下数值:
$$ p(体重=130|男性) = 5.9881 \times 10^{-6} $$
$$ p(脚掌=8|男性) = 1.3112 \times 10^{-3} $$
由于 $p(男性) = 0.5$ ,故这个人是男性的相对概率为:
$$ 0.5 \times 1.5789 \times 5.9881 \times 10^{-6} \times 1.3112 \times 10^{-3} = 6.1984 \times 10^{-9} $$
使用相同的方法,可以算出这个人为女性的相对概率为 $5.3778 \times 10^{-4}$。从数据可知,这个人为女性的概率比男性的概率高了 5 个数量级,故我们判断这个人为女性。
(完)