正则化
线性回归里的欠拟合和过拟合¶
- 欠拟合 (underfitting) 也叫做高偏差 (high bias) 。使用的特征过少导致成本函数过高。模型不能很好地拟合训练数据。
- 过拟合 (overfitting) 也叫高方差 (high variance) 。使用多个特征建模的预测函数非常完美地拟合了训练数据,其成本函数的值接近于零,但对新的数据预测时效果很差。
线性回归算法的欠拟合和过拟合
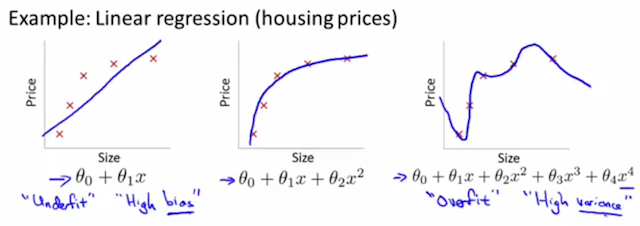
针对房价预测模型,左边是欠拟合的情况,右边是过拟合的情况。中间表示模型比较好的拟合了训练数据集。
逻辑回归算法的欠拟合和过拟合
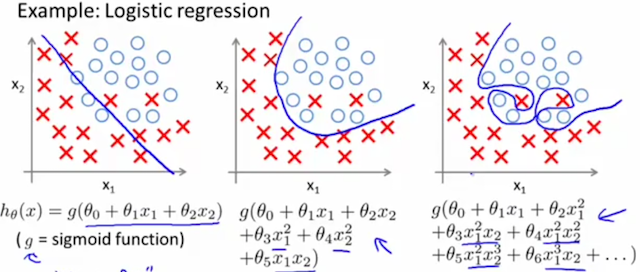
针对分类算法,左边是欠拟合,右边是过拟合,中间的模型比较好地拟合了训练数据集。
特征太多,而训练样本数据太少,则很可能出现过拟合。下面是一些解决过拟合问题的方法:
- 减少特征个数
- 手动减少特征个数
- 模型选择算法,比如主成份分析法 (PCA) 。主要原理就是把特征的重要性拿来排序,然后只选择前面几个权重比较大的特征,忽略排在后面的权重比较小的特征。
- 正则化
- 保留所有的特征,减小特征的权重 $\theta_j$ 的值。确保所有的特征对预测值都有少量的贡献。
- 当每个特征 $x_i$ 对预测值 $y$ 都有少量的贡献时,这样的模型可以良好地工作
这就是正则化的目的,为了解决特征过多时的过拟合问题。
正则化¶
$$ J(\theta) = \frac{1}{2m} \left[ \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 \right] + \lambda \sum_{j=1}^n \theta_j^2 $$
其中 $\lambda$ 的值有两个目的,即要维持对训练样本的拟合,又避免对训练样本的过拟合。如果 $\lambda$ 太大,则能确保不出现过拟合,但可能会导致对现有训练样本出现欠拟合。
怎么样从数学上理解正则化后的逻辑回归算法的成本函数解决了过拟合问题呢?
从数学角度来看,成本函数增加了一个正则项 $\lambda \sum_{j=1}^n \theta_j^2$ 后,成本函数不再唯一地与预测值与真实值的差距决定,还和参数 $\theta$ 的大小有关。有了这个限制之后,要实现成本函数最小的目的,$\theta$ 就不能随便取值了,比如某个比较大的 $\theta$ 值可能会让预测值与真实值的差距 $\left( h_\theta(x^{(i)}) - y^{(i)} \right)^2$ 值很小,但会导致 $\theta_j^2$ 很大,最终的结果是成本函数太大。这样,通过调节参数 $\lambda$ 就可以控制正则项的权重。从而避免线性回归算法过拟合。
利用正则化的成本函数,可以推导出参数迭代函数 (推导过程会用到一些微分运算法则):
$$ \begin{align} \theta_j & = \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m \left[ \left(\left(h(x^{(i)}) - y^{(i)}\right) x_j^{(i)}\right) + \frac{\lambda}{m} \theta_j \right] \\ & = \theta_j (1 - \alpha \frac{\lambda}{m}) - \alpha \frac{1}{m} \sum_{i=1}^m \left(\left(h(x^{(i)}) - y^{(i)}\right) x_j^{(i)}\right) \end{align} $$
$(1 - \alpha \frac{\lambda}{m})$ 因子在每次迭代时都将把 $\theta_j$ 收缩一点点。因为 $\alpha$ 和 $\lambda$ 是正数,而 m 是训练样例的个数,是个比较大的正整数。为什么要对 $\theta_j$ 进行收缩呢?因为加入正则项的成本函数和 $\theta_j^2$ 成正比,所以迭代时需要不断地试图减小 $\theta_j$ 的值。
通用方程的正则化¶
$$ \theta = (X^T X)^{-1} X^T y $$
这是还没有正则化的通用方程,我们用它来快速求解线性回归算法。下面是正则化的通用方程:
$$ \theta = (X^T X + \lambda Z)^{-1} X^T y $$
其中,Z 是 (n + 1) x (n + 1) 矩阵
$$ Z = \begin{bmatrix} 0 \\ & 1 \\ & & 1 \\ & & & \ddots \\ & & & & 1 \end{bmatrix} $$
正则化的通用方程实际上解决了两个问题。一个是确保不发生过拟合,另外一个也解决了 $X^T X$ 的奇异矩阵问题。当 m < n 时,$X^T X$ 将是一个奇异矩阵,使用 octave 里的 pinv 函数我们可以求出近似逆矩阵的值,但如果在其他编程语言里,是没有办法求出奇异矩阵的逆矩阵的。而从数学上可以证明,加上 $\lambda Z$ 后,结果将是一个非奇异矩阵。
通用方程的正则化公式推导过程极其复杂,过程从略。
逻辑回归成本函数的正则化¶
$$ J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^m y^{(i)} log(h_\theta(x^{(i)})) + (1 - y^{(i)}) log(1 - h_\theta(x^{(i)})) \right] + \frac{\lambda}{2m} \sum_{j=1}^n \theta_j^2 $$
相应地,正则化后的参数迭代公式
$$ \begin{align} \theta_j & = \theta_j - \alpha \frac\partial{\partial{\theta_j}}J(\theta) \\ & = \theta_j - \alpha \left[ \frac{1}{m} \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)} \right) x_j^{(i)} + \frac{\lambda}{m} \theta_j \right] \\ & = \theta_j (1 - \alpha \frac{\lambda}{m}) - \alpha \frac{1}{m} \sum_{i=1}^m \left(\left(h(x^{(i)}) - y^{(i)}\right) x_j^{(i)}\right) \end{align} $$
需要注意的是,上式中 $j \geq 1$,因为 $\theta_0$ 没有参与正则化。另外需要留意,逻辑回归和线性回归的参数迭代算法看起来形式是一样的,即公式 (4) 和公式 (7) 形式一样,但其实他们的算法是不一样的,因为两个式子的预测函数 $h_\theta(x)$ 是不一样的。针对线性回归,$h_\theta(x) = \theta^T x$,而针对逻辑回归 $h_\theta(x) = \frac{1}{1 + e^{-\theta^T x}}$。
根据正则化的,新的成本函数的参数迭代函数来实现 CostFunction,然后利用 octave 里的 fminunc 函数来求解,这样可以达到最高的运算效率。因为 fminunc 会使用优化过的梯度下降算法 Conjugate Gradient, BFGS, L-BFGS 等来提高运算效率。
学到这里,你基本上可以使用线性回归逻辑回归解决一些现实问题了。我看到硅谷有大量的公司使用机器算法来构建伟大的产品,那些机器学习工程师在这些公司获得了很好的职业发展并且赚了不少钱。— Andrew Ng
老师除了教得好,还要会鼓励,让学生保持学习的热情和兴趣。学完三周,热情可能会被消耗得差不多了,特别是第一次接触这些复杂数学公式的同学,听了老师的这个鼓励,瞬间满血复活有没有。仿佛走上硅谷机器学习工程师的职业道路了~~,等一下,先别叫醒我,让我的梦想飞一会儿。