支持向量机核函数
核函数¶
什么是核函数?核函数是特征转换函数。这是非常抽象的描述,这一节的内容就是为了理解这个抽象的概念的。
从多项式说起¶
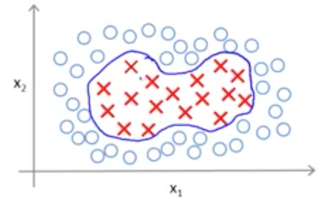
假设我们有一个非线性分界线的分类问题,有两个特征 $x_1, x_2$ ,回顾逻辑回归算法里的知识,我们可以使用多项式来增加特征,以便描述出非线性分界线。当:
$$ \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1 x_2 + \theta_4 x_1^2 + \theta_5 x_2^2 + … >= 0 $$
时,我们预测出 $y=1$。上述公式只写了二阶多项式,我们可以写到更高阶的多项式来模拟复杂的分界线。我们改写一下上面的公式:
$$ \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 + \theta_4 f_4 + \theta_5 f_5 + … >= 0 $$
这里,$f_1=x_1, f_2 = x_2, f_3 = x_1 x_2, f_4 = x_1^2, f_5 = x_2^2 …$ 。
那么问题来了,除了多项式外,有没有更好地途径把特征 $x_1, x_2$ 映射到特征 $f_1, f_2, f_3, f_4, f_5 …$ 呢?
相似性函数¶
我们在二维坐标上选择三个标记点 $l^{(i)}$ ,针对一个训练样例 $x$,我们使用相似性函数来定义新的特征:
$$ \begin{align} f_i &= similarity(x, l^{(i)}) \\ &= exp \left( - \frac{| x - l^{(i)} |^2}{2\sigma^2} \right) \\ &= exp \left( - \frac{\sum_{j=1}^n (x_j - l_j^{(i)})^2}{2\sigma^2} \right) \\ \end{align} $$
如下图所示,当我们选择三个标记点 $l^{(1)}, l^{(2)}, l^{(3)}$ 时,针对一个只有两个特征的训练样例 $(x_1, x_2)$,通过我们的相似性函数映射后,我们将得到 $f_1, f_2, f_3$ 三个新特征。
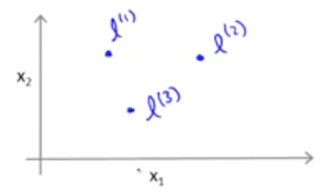
相似性函数的物理意义
$| x - l^{(i)} |^2$ 在二维平面上的物理意义是点 $x$ 到标记点 $l^{(i)}$ 的距离。从向量角度来理解,个是向量的范数。
高斯核函数
$$ f_i = exp \left( - \frac{\sum_{j=1}^n (x_j - l_j^{(i)})^2}{2\sigma^2} \right) $$
我们把上面的相似性函数称为高斯核函数,它的主要作用就是把输入特征映射到另外一组特征上。当 $x$ 离标记点 $l^{(i)}$ 很近的时候,这两个点间的距离接近于 0 ,故 $f_i$ 接近于 1 。当 $x$ 离标记点 $l^{(i)}$ 很远的时候,这两个点间的距离接近于无穷大,故 $f_i$ 接近于 0 。
理解相似性函数¶
假设我们选择了三个标识点 $l^{(1)}, l^{(2)}, l^{(3)}$ ,映射出三个新特征 $f_1, f_2, f_3$ ,那么当:
$$ \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 >= 0 $$
时,我们预测为 1。假设我们训练出来的参数为 $\theta_0 = -0.5, \theta_1 = 1, \theta_2 = 1, \theta_3 = 0$ ,那么当某个测试样例点 $x$ 靠近 $l^{(1)}$ ,但远离 $l^{(2)}, l^{(3)}$ 时,我们可以得出:
$$ \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 = -0.5 + 1 + 0 + 0 = 0.5 >= 0 $$
即我们把测试样例点 $x$ 归类到 $y=1$ 这个类别里。相同的道理,假设某个测试样例 $x$ 离三个标记点都很远,那么:
$$ \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 = -0.5 + 0 + 0 + 0 = -0.5 < 0 $$
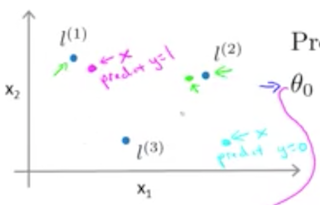
这样我们得出结论,把 $x$ 归类到 $y=0$ 这个类别里。使用相同的方法,最终我们针对所有的测试样例进行归类。
带核函数的支持向量机算法¶
选择标记点¶
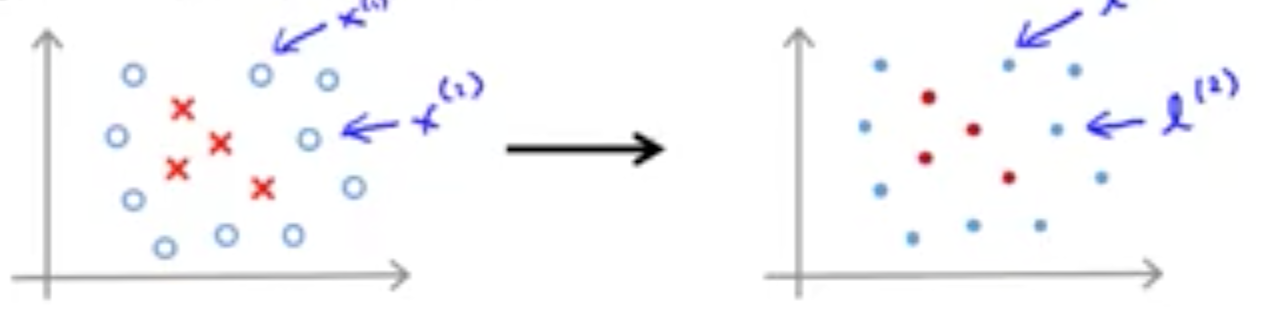
定义标记点 (landmark) 的一个很自然的方法是直接把 landmark 定义在训练数据集的训练样例上,即 $l^{(i)}=x^{(i)}$。那么给定一个新的交叉验证数据集或测试数据集里的样例 $x$,它与 landmark 的相似性函数,即高斯核函数如下
$$ f_i = similarity(x, l^{(i)}) = exp \left( - \frac{| x - l^{(i)} |^2}{2\sigma^2} \right) $$
针对训练样例,也满足上述核函数。由于我们选择 landmark 与训练样例重合,所以针对训练样例 $x^{(i)}$ 有 $f_i=1$ 。
计算预测值¶
假如我们已经算出了 $\theta$,那么当 $\theta^Tf >= 0$ 时,预测值为 1,反之为 0。
计算参数¶
根据 SVM 的成本函数,由于我们把 $f$ 代替 $x$ 作为新的特征,所以我们可以通过最小化下面的函数来计算得出参数 $\theta$
$$ J(\theta) = C \left[ \sum_{i=1}^m y^{(i)} cost_1(\theta^T f^{(i)}) + (1 - y^{(i)}) cost_0(\theta^T f^{(i)}) \right] + \frac{1}{2} \sum_{j=1}^n \theta_j^2 $$
针对上述公式,实际上 $m=n$,因为 $f$ 是由训练数据集 $x^{(i)}$ 定义,即 $f$ 是一个 m 维的向量。
支持向量机算法的参数¶
- C 值越大,越容易造成过拟合,即 lower bias, higher variance. 当 C 值越小,越容易造成欠拟合,即 higher bias, lower variance。
- $\sigma^2$ 越大,高斯核函数的变化越平缓,会导致 higher bias, lower variance。当 $\sigma^2$ 越小,高斯核函数变化越快,会导致 lower bias, higher variance。
实践中的 SVM¶
一般情况下,我们使用 SVM 库 (liblinear, libsvm …) 来求解 SVM 算法的参数 $\theta$,而不是自己去实现 SVM 算法。在使用这些库的时候,我们要做的步骤如下
- 选择参数 C
- 选择核函数
- 可以支持空的核函数,即线性核函数 (linear kernel)。Predict “y = 1” if $\theta^Tx >= 0$。
- 高斯核函数 $f_i = exp \left( - \frac{| x - l^{(i)} |^2}{2\sigma^2} \right)$,这个时候需要选择合适的参数 $\sigma^2$。
在使用第三方算法的时候,一般需要我们提供核函数的实现。输入参数是 $x_1, x_2$,输出为新的特征值 $f_i$。另外一个需要注意的点是,如果使用高斯核函数,在实现核函数时,需要对参数进行缩放,以便加快算法收敛速度。
多类别的分类算法¶
这个和逻辑回归里介绍的 one-vs.-all 一样。可以先针对一个类别和其他类别做二元分类,逐个分类出所有的类别。这样我们得到一组参数。假如,我们有 K 个类别,那么我们最终将得到 $\theta^{(1)}, \theta^{(2)}, \theta^{(3)} … \theta^{(K)}$ 个参数。
算法选择¶
逻辑回归和 SVM 都可以用来解决分类问题,他们适用的场景有些区别。
假设 n 是特征个数;m 是训练数据集的样例个数。一般可以按照下面的规则来选择算法。
如果 n 相对 m 来说比较大。比如 n = 10,000; m = 10 - 1000,如文本处理问题,这个时候使用逻辑回归或无核函数的 SVM 算法。 如果 n 比较小,m 中等大小。比如 n = 1 - 1000; m = 10 - 10,000。那么可以使用高斯核函数的 SVM 算法。 如果 n 比较小,m 比较大。比如 n = 1 - 1000; m = 50,000+ 。那么一般需要增加特征,并且使用逻辑回归或无核函数的 SVM 算法。
以上的所有情况都可以使用神经网络来解决。但训练神经网络的计算成本比较高。