支持向量机 SVM 算法
支持向量机算法 SVM 是 Support Vector Machine 的缩写,它是工业和学术界都有广泛应用的强大的算法。
从逻辑回归算法谈起¶
逻辑回归算法的预测函数¶
逻辑回归算法的预测函数称为 Sigmoid Function ,如下图:

这意味着,针对 $y=1$,我们希望预测值 $h(x) \approx 1$,那么只要 $z=\theta^T x \gg 0$ 即可。相同的道理,针对 $y=0$,我们希望预测值 $h(x) \approx 0$,那么只要 $z=\theta^T x \ll 0$ 即可。
逻辑回归算法的成本函数¶
回顾之前的知识,逻辑回归算法的成本函数如下
$$ J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^m y^{(i)} log(h_\theta(x^{(i)})) + (1 - y^{(i)}) log(1 - h_\theta(x^{(i)})) \right] + \frac{\lambda}{2m} \sum_{j=1}^n \theta_j^2 $$
如果我们去掉 $\frac{1}{m}$ 和累加器,同时暂时不考虑正则项,则可以得到另外一个样式的成本函数:
$$ J(\theta) = - y^{(i)} log(h_\theta(x^{(i)})) - (1 - y^{(i)}) log(1 - h_\theta(x^{(i)})) $$
当 $y^{(i)}=1$ 时,$1-y^{(i)}=0$,故这一式子再简化为:
$$ J(\theta) = - y^{(i)} log(h_\theta(x^{(i)})) = - log(\frac{1}{1 + e^{-z}}) $$
把上述函数以成本 J 为纵坐标,z 为横坐标,画出来的函数曲线如下:
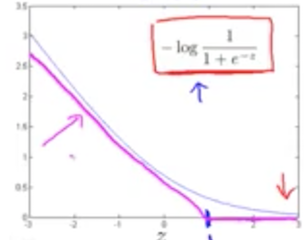
从图中可以看到,针对 $y=1$ 的情况,如果 $z=\theta^T x \gg 1$ 时,成本将很小。支持向量机的原理,就是简化逻辑回归算法的成本函数,以 $z=1$ 为分界线,当 $z<1$ 时,把成本函数简化为一条斜线,当 $z>=1$ 时,直接把成本简化为 0。如上图洋红色所示。
相同的道理,针对$y^{(i)}=0$ 时,变形后的逻辑回归算法成本函数简化为:
$$ J(\theta) = -(1 - y^{(i)}) log(1 - h_\theta(x^{(i)})) = - log(1 - \frac{1}{1 + e^{-z}}) $$
把上述函数以成本 J 为纵坐标,z 为横坐标,画出来的函数曲线如下:
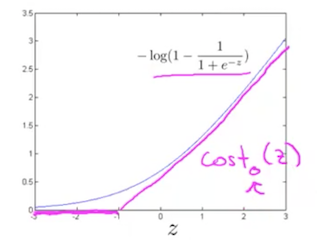
从图中可以看到,针对 $y=0$ 的情况,如果 $z=\theta^T x \ll -1$ 时,成本将很小。支持向量机的原理,就是简化逻辑回归算法的成本函数,以 $z=-1$ 为分界线,当 $z<-1$ 时,把成本函数简化为 0,当 $z>=-1$ 时,把成本简化一条斜线。如上图洋红色所示。
支持向量机算法的成本函数¶
根据上面的定义,支持向量机把成本函数分成两部分,一部分是针对 $y=1$ 的情况,它是一个以 $z=1$ 为分界点的折线。另外一部分是针对 $y=0$ 的情况,它是以 $z=-1$ 为分界点的折线。我们把这两个情况合并起来,并把正则项加上去,就得到支持向量机的成本函数:
$$ J(\theta) = C \left[ \sum_{i=1}^m y^{(i)} cost_1(\theta^T x^{(i)}) + (1 - y^{(i)}) cost_0(\theta^T x^{(i)}) \right] + \frac{1}{2} \sum_{j=1}^n \theta_j^2 $$
这就是用在支持向量机算法里的成本函数。这里的参数 C 越大,正则项的比重就越小,就容易造成过拟合。反之,如果 C 越小,正则项的比重就越大,就容易造成欠拟合。
支持向量机的预测函数¶
我们定义支持向量机的预测函数如下:
$$ h_\theta(x) = \begin{cases} 1, & \text{if $\theta^T x$ >= 1} \\ 0, & \text{if $\theta^T x$ <= -1} \\ \end{cases} $$
这里和逻辑回归算法比较,针对逻辑回归算法,其正负样本分界线为 $\theta^T x = 0$,即 $\theta^T x > 0$ 时为正样本,当 $\theta^T x < 0$ 时为负样本。而支持向量机的分类预测函数要求更严格,它要求 $\theta^T x >= 1$ 时为正样本,$\theta^T x <= -1$ 时为负样本。根据支持向量机的成本函数图形,只有这样成本才最小,即成本为零。如下图所示:
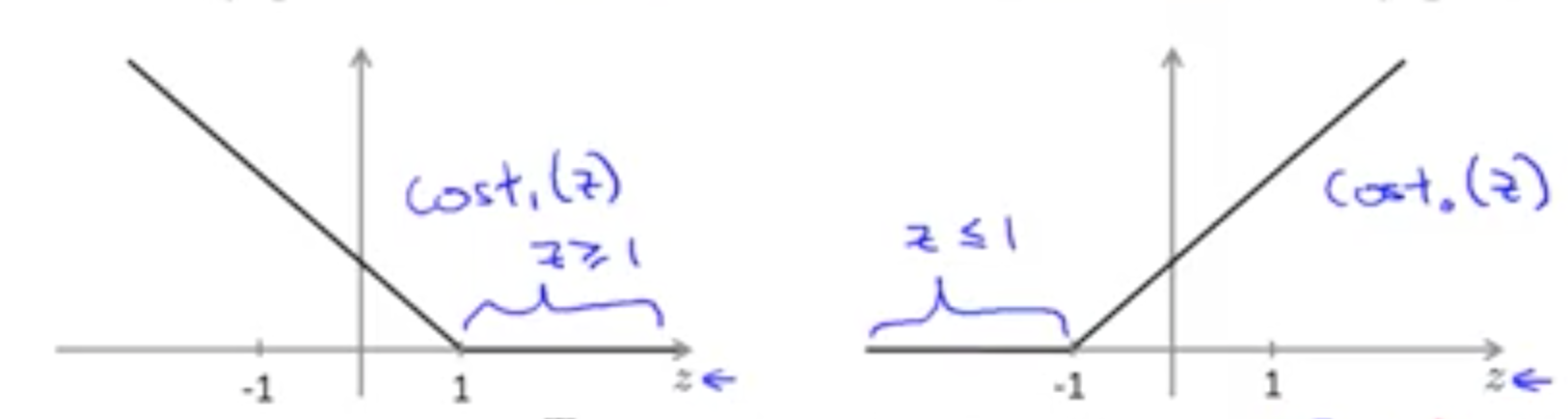
大间距分类算法¶
支持向量机也称为大间距分类算法。大间距的意思是,用 SVM 算法计算出来的分界线会保留对类别最大的间距,即有足够的余量。
我们看一个比较极端的情况,假设我们选取一个很大的值作为参数 C 的值,那么为了让成本最小,我们必须让成本函数的前半部分为 0,这样成本函数就只剩下:
$$ J(\theta) = \frac{1}{2} \sum_{j=1}^n \theta_j^2 $$
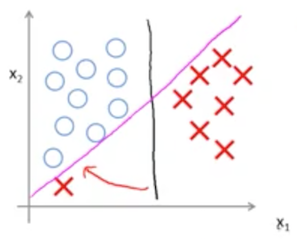
求解这个函数的结果,就会让我们获得一个较大间距的分类算法。如下图所示,假设我们有个分类问题。那么洋红色和绿色的都可以是合法的分界线,但 SVM 可以得到黑色的分界线,即确保到两个类别有最大的间距。
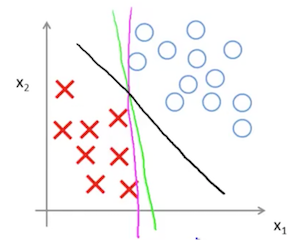
为什么求解 $J(\theta) = \frac{1}{2} \sum_{j=1}^n \theta_j^2$ 会得到最大间距的分界线呢?这个我们留到下面详细解释。
我们接着看下图,如果我们的参数 C 很大,那么可能发生过拟合,即左下角的一个异常的红色样例 X 可能会导致决策界从黑色线变成洋红色线。但实际上,直观地来理解,这样的转变是不合理的,我们仍然希望得到黑色的决策界。这个时候,我们可以调整参数 C ,让 C 的值不要太大,这样就不会被左下角的红色 X 异常样例的干扰,照样得到黑色的决策边界。
与逻辑回归算法类比,C 相当于 $\frac{1}{\lambda}$。通过调整 C 可以让 SVM 算法不至于过拟合,也不至于欠拟合。
从数学角度理解大间距分类算法¶
向量内积的几何含义¶
假设 u, v 是一个二维列向量,那么 $u^Tv$ 表示向量 v 在 向量 u 上的投影的长度。可以通过在二维平面上画出向量 u 和向量 v 来更清楚地看这个关系。
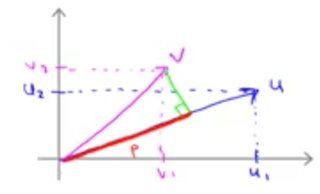
$$ u^T v = u_1 v_1 + u_2 v_2 = p |u| $$
其中 p 就是 v 在 u 上的投影的长度,它是有符号的实数;$|u|$ 是向量 u 的范数,即向量 u 的长度,其值为 $\sqrt{u_1^2 + u_2^2}$。
从数学上理解为什么支持向量机会把类别边界的间距做到最大¶
假设我们只有两个特征,即 n = 2,则 $J(\theta) = \frac{1}{2} \sum_{j=1}^n \theta_j^2$ 简化为:
$$ J(\theta) = \frac{1}{2} (\theta_1^2 + \theta_2^2) = \frac{1}{2} \left( \sqrt{\theta_1^2 + \theta_2^2} \right)^2 = \frac{1}{2} | \theta |^2 $$
回到 SVM 算法的预测函数:
$$ h_\theta(x) = \begin{cases} 1, & \text{if $\theta^T x$ >= 1} \\ 0, & \text{if $\theta^T x$ <= -1} \\ \end{cases} $$
即当预测为正样本时,我们需要 $\theta^T x >=1$,这个式子可以理解为向量内积,它的几何含义是x 在 $\theta$ 上的投影的长度大于等于 1,即 $p | \theta | >= 1$。如下图所示:
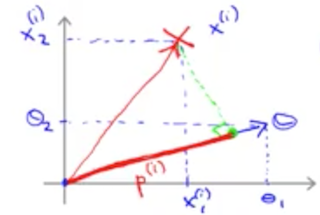
而我们的算法求解目标是使 $J(\theta) = \frac{1}{2} | \theta |^2$ 最小,所以 SVM 算法的求解目标就是要让 p 尽可能最大。即使所有的训练样例点 $x^{i}$ 到参数向量 $\theta$ 的投影长度最大。在几何上,决策边界和参数 $\theta$ 是正交的。如下图所示:
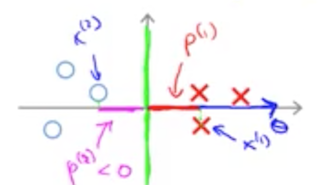
绿色线为决策边界,绿色线为 $\theta$ 所代表的向量。那么 SVM 的求解目标就是让各个训练样例的点 $x^{i}$ 到 $\theta$ 上的投影长度最大。上图中,我们可以试着换一个决策边界,试着画出训练样例到这个新的决策边界所决定的参数 $\theta$ 的投影长度,即可理解为什么 SVM 可以让决策边界得到最大的间距。